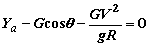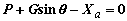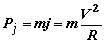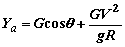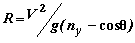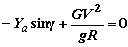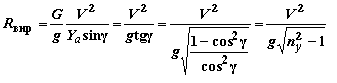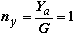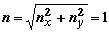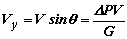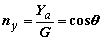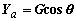6.3. Пространственное движение самолета 

    Рассмотрим простейшие случаи движения самолета.
    В первом приближении можно считать, что криволинейный маневр в вертикальной плоскости («горка») (рис. 6.5,а) происходит по дуге окружности радиуса R за счет центростремительной силы Y_a, которая численно равна сумме проекции силы тяжести G на ось Y и инерционной центробежной силы P_j, стремящейся сохранить прямолинейное движение самолета.
    Можно записать (рис. 6.5,б) условие равновесия (суммы проекций всех сил на оси 0Y и 0X равны нулю):  

;

   При скорости полета V и радиусе кривизны R центробежная сила

   где  m=G/g  – масса самолета, кг.
   Тогда 

    Разделив это выражение на силу тяжести, получим:

    Маневр в горизонтальной плоскости (рис. 6.6,а) требует создания центростремительной силы, направленной к центру кривизны траектории и равной по модулю центробежной силе. Создание такой силы возможно за счет накренения самолета на угол (рис. 6.6,б). В этом случае вертикальная составляющая подъемной силы Y_acosg уравновешивает силу тяжести, а горизонтальная составляющая R_п= Y_asing – центробежную силу P_j=GV²/gR, и условия равновесия имеют вид:

Yacosg - G=0 ;

    Под действием этих сил самолет будет осуществлять установившийся разворот (правильный «вираж», франц. virage, от virer – поворачивать) со скоростью V по дуге окружности радиуса R.
    Отсюда G = Y_acosg, и перегрузка в вертикальной плоскости n_y = Y_a/G = 1/cosg, т. е. чем больше угол крена на вираже, тем больше перегрузка n_y.
    Радиус виража может быть определен как

    Впервые в мире правильный разворот на самолете в горизонтальной плоскости с креном (вираж) и замкнутую кривую в вертикальной плоскости («мертвую петлю») выполнил в 1913 году замечательный русский летчик П.Н. Нестеров, доказав тем самым возможность безопасно совершать на самолете любые эволюции в воздухе и положив начало высшему пилотажу.
    Легко видеть, что чем большую перегрузку можно создать на самолете, тем меньше будет радиус кривизны траектории, т. е. тем энергичнее будет маневр.
  

Рис. 6.7. Предельные перегрузки, переносииые человеком

  Маневренные возможности пилотируемых ЛА ограничиваются способностью людей, находящихся на его борту, переносить перегрузки. В зависимости от направления центростремительного ускорения субъективная сила тяжести человеческого тела (его вес) может быть больше нормального (положительная перегрузка), обращаться в нуль (невесомость) и принимать отрицательные значения (отрицательная перегрузка).
    При выходе самолета из пикирования, когда инерционная сила направлена вниз, летчика прижимает к сиденью, на него действует положительная перегрузка в направлении голова - таз.
    При входе самолета в пикирование, когда инерционная сила направлена вверх, летчика отрывает от сиденья, на него действует отрицательная перегрузка в направлении таз - голова.
    

Рис. 6.8. Силы, действующие на самолет в горизонтальном полет

На рис. 6.7 показаны предельные перегрузки n в различных направлениях, переносимые человеком в зависимости от продолжительности их действия t. Переносимость перегрузки связана с механическим воздействием опоры (кресла, сиденья, ложемента) на тело человека, с приливами и отливами крови (с нарушением мозгового кровообращения).
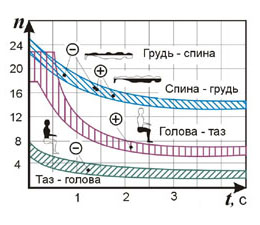
    Рис. 6.7 объясняет, почему космонавты возвращаются на Землю в летательных аппаратах с низким аэродинамическим качеством (т. е. по баллистическим траекториям) лежа в специальных креслах спиной к направлению полета – при таком положении тела легче всего переносить перегрузки.
Тренированные люди в специальных противоперегрузочных костюмах (см. главу 15) способны переносить достаточно высокие перегрузки в течение длительного времени. Поэтому маневренные самолеты (например, перехватчики) могут достигать эксплуатационных перегрузок порядка 10–13.

Рис. 6.9. Силы, действующие на самолет при наборе высоты

Для неманевренных самолетов (пассажирские, самолеты для транспортировки грузов) эксплуатационные перегрузки не превышают 2.
    Основным режимом для неманевренных самолетов является горизонтальный полет.
    Рассматривая схему сил, действующих на самолет в горизонтальном полете (рис. 6.8), запишем проекции вектора перегрузки на оси координат: 

 Отсюда 

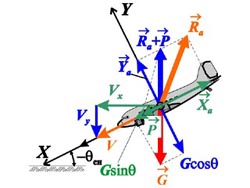
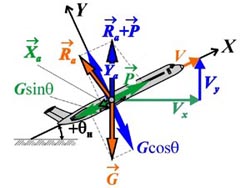
    Для режима набора высоты с постоянной скоростью (рис. 6.9) Y_a = Gcosq; P = X_a+Gsinq , где q – угол наклона траектории.
    Видно, что подъемная сила самолета уравновешивает только часть силы тяжести Gcosq.
    Следовательно, набор высоты происходит за счет избытка тяги двигателя ΔP=Gsinq.
    Скороподъемность – вертикальную скорость при наборе высоты – определим из соотношения 

    Проекции вектора перегрузки на оси координат:

;

    Отсюда 

    Следует отметить, что на режиме набора высоты q > 0 и n_x > 0 .

Рис. 6.10. Силы, действующие на самолет при снижении

    Для режима снижения (рис. 6.10) 

    Видно, что снижение происходит за счет недостатка тяги двигателя P = Gsinq.
    Для проекций вектора перегрузки запишем n_x = cosq; n_y = sinq. Отметим, что на режиме снижения q < 0 и n_x < 0.
    Однако  

    Следовательно, на основных режимах полета пассажирского самолета – в горизонтальном полете, при наборе высоты и снижении – перегрузка