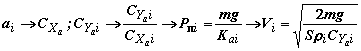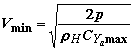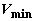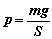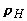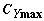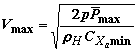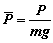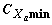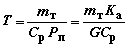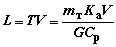6.4. Понятие об аэродинамическом расчете  

    Методы динамики полета позволяют дать рекомендации по технике пилотирования самолета, подобрать наивыгоднейшие режимы полета, рассчитать летно-технические характеристики (ЛТХ) самолета. Определение основных ЛТХ самолета принято называть аэродинамическим расчетом.
    Н.Е. Жуковский предложил для определения ЛТХ метод тяг (метод Н.Е. Жуковского), основанный на сопоставлении потребной для полета тяги Pп с располагаемой тягой Pp двигателей, установленных на самолете (рис. 6.11). Кривая располагаемых тяг Pp определяется характеристиками двигателя. Кривая потребных тяг получается расчетом в диапазоне летных углов атаки для каждого угла атаки по алгоритму:

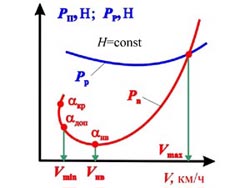
    По результатам сравнения кривой потребных и располагаемых тяг определяется диапазон высот и скоростей полета, который способен реализовать проектируемый самолет (рис. 6.12).

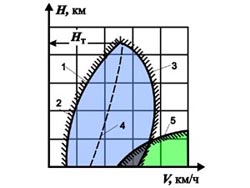Рис6.11. Кривые потребных и
располaгаемых тяг.

Рис 6.12.Диапазон летных высот
и скоростей.
    Зона 1 реализуемых высот и скоростей полета самолета (область возможных полетов) ограничена минимально допустимыми 2 и максимально допустимыми 3 скоростями полета.
Граница 2 минимальной скорости полета Vmin определится из уравнения горизонтального полета Ya = G  как
где:
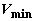
- минимальная скорость полета, м/с;
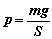
- удельная нагрузка на крыло самолета с полетной массой m и площадью крыла S,Па
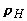
- плотность воздуха на высоте H, кг/м3
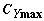
- Максимально допустимый в полете коэффициент подьемной силы самолета 
 

    Граница 3 максимальной скорости полета Vmax определится максимальной тягой двигателя из уравнения горизонтального полета Xa=P как

где:
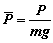
- удельная тяговооруженность самолета с полетной массой m и тягой двигателя P
p - удельная нагрузка на крыло самолета, Па
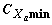
- минимальный коэффициент лобового сопротивления при полете на данной высоте

    Наивыгоднейшая скорость полета Vнв (кривая 4 на рис. 6.12) соответствует максимальному аэродинамическому качеству самолета Kmax и, следовательно, минимально потребной для полета тяговооруженности, поскольку P=1/Ka
    Наивыгоднейшей скорости полета соответствует и максимальная скороподъемность Vy, определяемая избытком тяги двигателя, которую можно использовать для набора высоты.
   Пересечение границ 2 и 3 определит теоретический потолок самолета Нт, на котором Vmax = Vmin, т. е. возможен полет с единственной скоростью, разгон самолета невозможен и, следовательно, Vy= 0.
   Практический потолок самолета Нп определяется высотой, на которой вертикальная скорость соответствует какой-либо заранее установленной величине, например Vy = 0,5 м/с.
   Динамический потолок самолета - высота, которой достигает самолет в результате энергичного вертикального маневра (горки) после разгона до большой горизонтальной скорости, используя для набора высоты не только тягу двигателей, но и кинетическую энергию, накопленную при разгоне.
   Полет в болтанку, когда на человека действуют значительные знакопеременные нагрузки, вызванные порывами ветра, заставляет ограничивать диапазон скоростей и высот полета. На рис. 6.12 граница 5 обусловлена переносимостью человеком перегрузок при полете в турбулентной атмосфере.
   В первом приближении продолжительность Т и дальность L полета определятся как

;
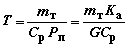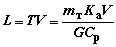где
T - продолжительность полета, ч;
mt - запас топлива на борту самолета, кг;
Cp -  удельный расход топлива, килограмм массы топлива на ньютон тяги в час   (т. е. количество топлива в килограммах, потребное для создания двигателем силы тяги в 1 Н в течение 1 ч полета)
Pп -  потребная тяга двигателей, H;
K a -  аэродинамическое качество самолета;
G -  сила тяжести (вес) самолета;
m -  полетная масса самолета, кг;
g -  ускорение свободного падения, м/с2;
L -  дальность полета, км;
V -  скорость полета, км/ч

    В реальном полете ЛА совершают сложные, неустановившиеся движения, когда параметры движения изменяются во времени. Поэтому необходимо при проектировании рассматривать пространственные траектории ЛА при воздействии на него переменных во времени управляющих и возмущающих воздействий.
   Естественно, что решение подобных задач требует применения значительно более сложного математического аппарата, чем тот, которым мы воспользовались при рассмотрении сил, действующих на самолет, и расчете его ЛТХ.

Предыдущая глава | Предыдущий параграф Следующая глава  
ОГЛАВЛЕНИЕ

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ