10.3.5. Изгиб

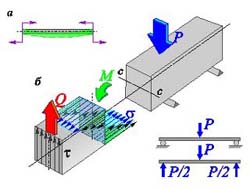
   Схема нагружения изгибом показана на рис. 10.21,а. Внешние силы, образующие момент относительно оси с-с, перпендикулярной продольной оси балки, вызывают деформации, которые заключаются в искривлении продольной оси балки. Такой вид деформированного состояния называют чистым изгибом.
   В технике широко распространен изгиб элементов конструкции, вызванный приложением к ним сосредоточенной силы или распределенной нагрузки (см. раздел 8.1, рис. 8.1-8.8).

Рис. 10.21. Изгиб балки прямоугольного сечения	Рис. 10.22. Уравновешивание балки при поперечной нагрузке

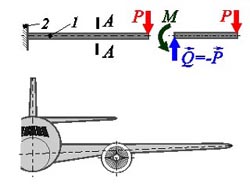
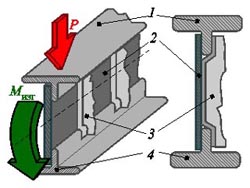
   Для простейшей балки прямоугольного сечения (рис. 10.21,б), нагруженной сосредоточенной силой, деформированное состояние характеризуется наличием нормальных σ и касательных τ напряжений в любом поперечном сечении. Выпуклая сторона балки растянута, вогнутая - сжата. Зоны растяжения и сжатия разделены нейтральным слоем, длина которого при изгибе остается неизменной и нормальные напряжения в котором отсутствуют.
   Статическое равновесие балки под поперечной нагрузкой обеспечивают нормальные напряжения σ, создающие уравновешивающий момент М, и касательные напряжения τ, создающие уравновешивающую перерезывающую силу Q. Это можно проследить, рассматривая равновесие по сечению А-А (рис. 10.22) консольной балки 1, заделанной на опору 2.
   Как и в случае с кручением (см. рис. 10.19,в), сплошное поперечное сечение конструктивного элемента, работающего на изгиб, нерационально, так как вблизи нейтрального слоя материал недогружен.
   Наиболее рациональным будет сечение (рис. 10.23), в котором основная масса материала сосредоточена в зонах, максимально удаленных от нейтральной оси, - в поясах 1 и 4, которые, работая на растяжение (пояс 1) и сжатие (пояс 4), создают уравновешивающий изгибающий момент М_изг. Тонкая стенка 2, соединяющая пояса и подкрепленная стойками 3, работая на сдвиг, создает уравновешивающую перерезывающую силу Р.
   Различные внешние нагрузки, которые одновременно действуют на ЛА, стремясь деформировать и, в пределе, разрушить конструкцию, создают в ней весь спектр внутренних сил.

Рис. 10.23. Тонкостенная балка	Рис. 10.24. Уравновешивание крыла

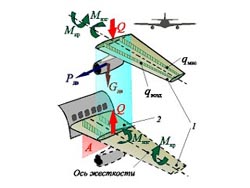
   Так, (рис. 10.24) под действием распределенных воздушной q_возд и массовой q_мас нагрузок и сосредоточенных сил тяги Р_дв и веса G_дв двигателя в любом произвольно взятом сечении крыла (например, плоскостью А) возникнут внутренние силовые факторы: перерезывающая сила Q, изгибающий М_изг и крутящий М_кр моменты, которые будут уравновешивать условно отсеченную (концевую) часть крыла 1. Равные им, но противоположные по направлению силовые факторы для оставшейся (внутренней) части крыла 2 будут являться внешними нагрузками, заменяя отсеченную часть крыла.
   В первом приближении можно не учитывать напряженно-деформированное состояние крыла под действием силы лобового сопротивления Х и силы тяги двигателя Р_дв, стремящихся изогнуть конструкцию крыла в плоскости хорд, поскольку очевидно, что жесткость на изгиб крыла в этом направлении значительно больше, чем жесткость на изгиб "из плоскости" (в вертикальном направлении). Кроме того, силы, действующие на крыло в горизонтальной плоскости, значительно меньше.
   Напомним, что в горизонтальном установившемся полете

Х = Y/К и Р_дв = G/(Kn_дв) = Y/(Kn_дв),